Flush In Crib Hand
Traditional Cribbage is a card game that has been around since the 17th Century. It involves creating hands composed of pairs, runs, flushes, and sums to 15. Here at eCribbage.com, you can play 2 player, 3 player, and 4 player games. You can also play teams, muggins, and jokers.
Flush In Your Hand Crib
What features make eCribbage.com the best?
These are standard hand rankings for most poker games and apply to all high-hand poker variations including Texas Hold'em, Omaha and Stud. You'll find a printable poker hand rankings chart below the hand rankings as well as answers to some of the most frequently asked questions about poker hands and poker hand ranking. If the dealer is discarding for the crib, they should “salt” it with the best possible cards, but at the same time retain good cards in their hand that can be used for high scoring. Conversely, for the non-dealer, it is best to lay out cards that will be the least advantageous for the dealer.
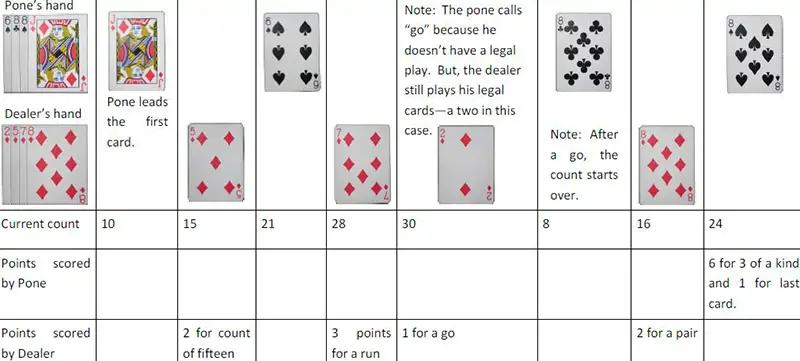
How to play (2 player):
The players cut to see who gets the first 'crib'. Players are dealt 6 cards each, and both have to discard 2 cards into the crib. Then a community card is cut that will play for both hands in the show. If a jack is cut for the cut card, the player with the crib immediately gets 2 points. (This is called His Nobs). Now on to the play:
The play
Players take turns playing (pegging) their cards one at a time and announcing the total sum of the cards. Face cards count for 10. If the sum is equal to 15 or 31, that player gets 2 points. If the player forms a pair, they get 2 points. A triple pair is worth 6 points, and a quadruple pair is worth 12 points. If either player forms a run of 3 or more, they get to claim that many points as well. Runs do not necessarily have to be played in order. For example if 4,7,5,6 was played, whoever laid the 6 would get to claim a run for 4 points.
You are not allowed to play a card to make a sum over 31, so if you play to 28 and your opponent only has cards of over 3, they will say GO and you will continue to play as many cards as you can up to 31. You also claim one point for playing the last card of every trick. Whoever played the last card in the trick, their opponent starts the next trick. When all cards have been played, you move on to the show.
The show
The show is where you count all the hands up. The player that does not have the crib counts first, then the player with the crib counts their hand, and then finally the crib is counted. Scores count for the following:
How to play (3 player):
3 player crib is very similar to 2 player crib except players are dealt 5 cards each instead of 6. They only throw one card each to the crib, and one card is taken off the top of the deck and placed in the crib.
eCribbage.com also provides the variant where the dealer (the player with the crib) can deal themself 6 cards, and the rest of the players 5. The dealer throws 2 cards to their crib, and the rest of the players throw 1 card to the crib.
How to play (4 player):
4 player crib is very similar to 2 player crib except players are dealt 5 cards each instead of 6. Every player throws one card to the crib. The play goes clockwise through all players. There is also a 2 vs 2, team cribbage game that is described on the team cribbage page.
In cribbage, the probability and maximum and minimum score of each type of hand can be computed.
Distinct hands[edit]
- There are 12,994,800 possible hands in Cribbage: 52 choose 4 for the hand, and any one of the 48 left as the starter card.
Flush In Crib Handle
- Another, and perhaps more intuitive way of looking at it, is to say that there are 52 choose 5 different 5-card hands, and any one of those 5 could be the turn-up, or starter card.
Therefore, the calculation becomes:
- 1,009,008 (approximately 7.8%) of these score zero points,[1] or 1,022,208 if the hand is the crib, as the starter must be the same suit as the crib's four cards for a flush.
- Not accounting for suit, there are 14,715 unique hands.[2]
Maximum scores[edit]

- The highest score for one hand is 29: 555J in hand with the starter 5 of the same suit as the Jack (8 points for four J-5 combinations, 8 points for four 5-5-5 combinations, 12 points for pairs of 5s and one for his nob).
- The second highest score is 28 (hand and starter together comprise any ten-point card plus all four 5s, apart from the 29-point hand above).
- The third highest score is 24 (A7777, 33339, 36666, 44447, 44556, 44566, 45566, 67788 or 77889).
- The highest score as a dealer from the hand and crib is 53. The starter must be a 5, the hand must be J555, with the Jack suit matching the starter (score 29), and the crib must be 4466 (score 24), or vice versa.
- The highest number of points possible (excluding pegging points) in one round is 77. The dealer must score 53, the opponent must then have the other 4466 making another 24 point hand for a total of 77.
- The highest number of points from a hand that has a potential to be a '19 hand' is 15. It is a crib hand of one suit, 46J and another ten card, with a 5 of that suit cut up. The points are 15 for 6, a run for 9, nobs for 10, and a flush for 15. Any of the following cards in an unlike suit yields a '19 hand'; 2,3,7,8,and an unpaired ten card.
- The most points that can be pegged by playing one card is 15, by completing a double pair royal on the last card and making the count 15: 12 for double pair royal, 2 for the 15, and 1 for the last card. This can happen in two ways in a two-player game. The non-dealer must have two ten-value cards and two 2s, and the dealer must have one ten-value card and 722, in which case the play must go: 10-10-10-go; 7-2-2-2-2. For example:
| Alice (dealer) |
|---|
| Bob |
| Player | Card | Cumulative | Score | Announced |
|---|---|---|---|---|
| Bob | 10 | 'ten' | ||
| Alice | 20 | 'twenty' | ||
| Bob | 30 | 3 points (run) | 'thirty' | |
| Alice | 1 point to Bob (30 for one) | 'go' | ||
| Alice | 7 | 'seven' | ||
| Bob | 9 | 'nine' | ||
| Alice | 11 | 2 points | 'eleven for two' | |
| Bob | 13 | 6 points | 'thirteen for six' | |
| Alice | 15 | 15 points (double pair royal, fifteen, last card) | 'fifteen for fifteen' |
- Alternatively, the players can each have two deuces, with one also holding A-4 and the other two aces. Then play might go 4-A-A-A-2-2-2-2.
- The maximum number of points that can be scored in a single deal by the dealer in a two player game is 78 (pegging + hand + crib):
Non-dealer is dealt 3 3 4 4 5 J and Dealer is dealt 3 3 4 4 5 5. Non-dealer discards J 5 to the crib (as ill-advised as this may be). Dealer discards 5 5 to the crib. Note that the J is suited to the remaining 5. The remaining 5 is cut.
Play is 3 3 3 3 4 4 4 4 go. The dealer scores 29 total peg points.
The dealer's hand is 3 3 4 4 5 = 20
The dealer's crib is J(nobs) 5 5 5 5 = 29
The total score for the dealer is 29 + 20 + 29 = 78.
Note that the correct play for both players is to keep 3 3 4 5 worth 10 points and discarding J 4 and 4 5 to the crib respectively, meaning in reality, this hand would never take place. A more realistic hand would be both players being dealt 3 3 4 4 J J with both discarding J J and a 5 cut. In this case, with pegging as described above, the total score would be 20 (hand) + 21 (crib) + 29 (pegging) = 70 points. - The maximum number of points that can be scored in a single deal by the non-dealer in a two player game is 48 (pegging + hand), with the following example :
Non-dealer is dealt 5 5 4 4 crib crib and Dealer is dealt 4 4 5 9 crib crib. Cut card is a 6.
Play is 5 5 5 4 4 4 4, with the Non-dealer pegging 24. The Non-dealer scores 24 in the hand for a total of 48 points. - The maximum number of points that can be scored with a four-card flush is 21, which is achieved with a hand of 5 5 10 J Q or 5 5 J Q K: a pair, six fifteens, a three-card sequence, and the flush. A five-card flush of 5 10 J Q K scores 18 if the Jack is not the starter.
Minimum scores[edit]
- The dealer in two-player, 6-card cribbage will always peg at least one point during the play (the pegging round), unless the opponent wins the game before the pegging is finished. If non-dealer is able to play at each turn then dealer must score at least one for 'last'; if not, then dealer scores at least one for 'go'.
- While 19 is generally recognized as 'the impossible hand', meaning that there is no combination of 5 cards that will produce a score of 19 points, scores of 25, 26, 27, and greater than 29 are also impossible in-hand point totals.[1] Sometimes if a player scores 0 points in their hand they will claim they have a '19-point hand.'[3]
Minimum while holding a 5[edit]
If a player holds a 5 in their hand, that player is guaranteed at least two points, as shown below:
A 0-point hand must have five distinct cards without forming a run or a fifteen combination. If such a hand includes a 5, it cannot hold a 10 or a face card. It also cannot include both an A and a 9; both a 2 and an 8; both a 3 and a 7; or both a 4 and a 6. Since four more cards are needed, exactly one must be taken from each of those sets. Let us run through the possible choices:
- If the hand includes a 9, it cannot hold a 6, so it must hold a 4. Having both a 4 and a 9, it cannot hold a 2, so it must hold an 8. Holding both a 4 and an 8, it cannot hold a 3, so it must hold a 7. But now the hand includes a 7-8 fifteen, which is a contradiction.
- Therefore, the hand must include an A. If the hand includes a 7, it now cannot contain an 8, as that would form a 7-8 fifteen. However it cannot hold a 2, as that would form a 7-5-2-A fifteen. This is a contradiction.
- Therefore, the hand must include a 3. Either a 2 or a 4 would complete a run, so the hand must therefore include a 6 and an 8. But this now forms an 8-6-A fifteen, which is a contradiction.
Therefore, every set of five cards including a 5 has a pair, a run, or a fifteen, and thus at least two points.
Interestingly, a hand with two 5s also can score only two points; an example is 2 5 5 7 9, which would be most likely a crib hand, and would not score a flush because of the pair, although said hand can be a non-crib four-card flush if either 5 is the starter. A hand with three 5s scores at least eight points; a hand with all four 5s scores 20 points and is improved only with a 10, J, Q, or K (scoring 28 except for the 29 hand previously described.)
It is also true that holding both a 2 and a 3, or an A and a 4 (pairs of cards adding up to five) also guarantees a non-zero score:
- If a hand includes both a 2 and a 3 and is to score 0 points, it cannot have a face card, an A, a 4, or a 5. This requires three cards from the 6, 7, 8, and 9, and any such selection will include a fifteen.
- If a hand includes both an A and a 4 and is to score 0 points, it cannot have a face card or a 5. It also cannot have both a 2 and a 3; both a 6 and a 9; or both a 7 and an 8. If the hand includes a 2, it cannot have a 9 (9-4-2 fifteen). Thus it must have a 6. It then cannot have an 8 (8-4-2-A fifteen) or a 7 (7-6-2 fifteen). If, however, the hand includes a 3, it cannot include an 8 (8-4-3 fifteen) or a 7 (7-4-3-A fifteen). These are all contradictions, so every hand containing both an A and a 4 scores at least two points.
Odds[edit]
- The table below assumes the card(s) discarded to the crib are randomly chosen. Given this assumption, the odds of getting a 28 hand in a two-player game are about 1 in 170984, and a perfect 29 hand 1 in 3,248,700.[3]
- However, if we assume that the player will always keep J555 if those cards are included in the hand, the odds of getting a perfect 29 hand starting with a six-card hand are 1 in 216,580, while the odds after discarding from a five-card hand are 1 in 649,740.[4]
Flush In Crib Hand
Scoring Breakdown, assuming random discard(s) to the crib[1]
| Score | Number of hands (out of 12,994,800) | Percentage of hands | Percentage of hands at least as high |
|---|---|---|---|
| 0 | 1,009,008 | 7.7647 | 100 |
| 1 | 99,792 | 0.7679 | 92.2353 |
| 2 | 2,813,796 | 21.6532 | 91.4674 |
| 3 | 505,008 | 3.8862 | 69.8142 |
| 4 | 2,855,676 | 21.9755 | 65.928 |
| 5 | 697,508 | 5.3676 | 43.9525 |
| 6 | 1,800,268 | 13.8538 | 38.5849 |
| 7 | 751,324 | 5.7817 | 24.7311 |
| 8 | 1,137,236 | 8.7515 | 18.9494 |
| 9 | 361,224 | 2.7798 | 10.1979 |
| 10 | 388,740 | 2.9915 | 7.4181 |
| 11 | 51,680 | 0.3977 | 4.4266 |
| 12 | 317,340 | 2.4421 | 4.0289 |
| 13 | 19,656 | 0.1513 | 1.5868 |
| 14 | 90,100 | 0.6934 | 1.4355 |
| 15 | 9,168 | 0.0706 | 0.7421 |
| 16 | 58,248 | 0.4482 | 0.6715 |
| 17 | 11,196 | 0.0862 | 0.2233 |
| 18 | 2,708 | 0.0208 | 0.1371 |
| 19 | 0 | 0 | 0.1163 |
| 20 | 8,068 | 0.0621 | 0.1163 |
| 21 | 2,496 | 0.0192 | 0.0542 |
| 22 | 444 | 0.0034 | 0.0350 |
| 23 | 356 | 0.0027 | 0.0316 |
| 24 | 3,680 | 0.0283 | 0.0289 |
| 25 | 0 | 0 | 0.0006 |
| 26 | 0 | 0 | 0.0006 |
| 27 | 0 | 0 | 0.0006 |
| 28 | 76 | 0.0006 | 0.0006 |
| 29 | 4 | 0.00003 | 0.00003 |
- Mean = 4.7692
- Standard deviation = 3.1254
- Skewness = 0.9039
- Excess kurtosis = 1.4599
Note that these statistics do not reflect frequency of occurrence in 5 or 6-card play. For 6-card play the mean for non-dealer is 7.8580 with standard deviation 3.7996, and for dealer is 7.7981 and 3.9082 respectively. The means are higher because the player can choose those four cards that maximize their point holdings. For 5-card play the mean is about 5.4.
Slightly different scoring rules apply in the crib - only 5-point flushes are counted, in other words you need to flush all cards including the turn-up and not just the cards in the crib. Because of this, a slightly different distribution is observed:
Scoring Breakdown (crib/box hands only)
| Score | Number of hands (+/- change from non-crib distribution) (out of 12,994,800) | Percentage of hands | Percentage of hands at least as high |
|---|---|---|---|
| 0 | 1,022,208 (+13,200) | 7.8663 | 100 |
| 1 | 99,792 (0) | 0.7679 | 92.1337 |
| 2 | 2,839,800 (+26,004) | 21.8534 | 91.3658 |
| 3 | 508,908 (+3,900) | 3.9162 | 69.5124 |
| 4 | 2,868,960 (+13,284) | 22.0778 | 65.5962 |
| 5 | 703,496 (+5,988) | 5.4137 | 43.5184 |
| 6 | 1,787,176 (-13,092) | 13.7530 | 38.1047 |
| 7 | 755,320 (+3,996) | 5.8125 | 24.3517 |
| 8 | 1,118,336 (-18,900) | 8.6060 | 18.5393 |
| 9 | 358,368 (-2,856) | 2.7578 | 9.9332 |
| 10 | 378,240 (-10,500) | 2.9107 | 7.1755 |
| 11 | 43,880 (-7,800) | 0.3377 | 4.2648 |
| 12 | 310,956 (-6,384) | 2.3929 | 3.9271 |
| 13 | 16,548 (-3,108) | 0.1273 | 1.5342 |
| 14 | 88,132 (-1,968) | 0.6782 | 1.4068 |
| 15 | 9,072 (-96) | 0.0698 | 0.7286 |
| 16 | 57,288 (-960) | 0.4409 | 0.6588 |
| 17 | 11,196 (0) | 0.0862 | 0.2179 |
| 18 | 2,264 (-444) | 0.0174 | 0.1318 |
| 19 | 0 (0) | 0 | 0.1144 |
| 20 | 7,828 (-240) | 0.0602 | 0.1144 |
| 21 | 2,472 (-24) | 0.0190 | 0.0541 |
| 22 | 444 (0) | 0.0034 | 0.0351 |
| 23 | 356 (0) | 0.0027 | 0.0317 |
| 24 | 3,680 (0) | 0.0283 | 0.0289 |
| 25 | 0 (0) | 0 | 0.0006 |
| 26 | 0 (0) | 0 | 0.0006 |
| 27 | 0 (0) | 0 | 0.0006 |
| 28 | 76 (0) | 0.0006 | 0.0006 |
| 29 | 4 (0) | 0.00003 | 0.00003 |
- Mean = 4.7348
As above, these statistics do not reflect the true distributions in 5 or 6 card play, since both the dealer and non-dealer will discard tactically in order to maximise or minimise the possible score in the crib/box.
Card combinations[edit]
- A hand of four aces (AAAA) is the only combination of cards wherein no flip card will add points to its score.
- There are 71 distinct combinations of card values that add to 15:
| Two cards | Three cards | Four cards | Five cards | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| X5 96 87 | X4A X32 95A 942 933 | 86A 852 843 77A 762 | 753 744 663 654 555 | X3AA X22A 94AA 932A 9222 85AA | 842A 833A 8322 76AA 752A 743A | 7422 7332 662A 653A 6522 644A | 6432 6333 554A 5532 5442 5433 4443 | X2AAA 93AAA 922AA 84AAA 832AA 8222A 75AAA | 742AA 733AA 7322A 72222 66AAA 652AA 643AA | 6422A 6332A 63222 553AA 5522A 544AA 5432A | 54222 5333A 53322 4442A 4433A 44322 43332 |
| Note: 'X' indicates a card scoring ten: 10, J, Q or K | |||||||||||
Hand and Crib statistics[edit]
If both the hand and the crib are considered as a sum (and both are drawn at random, rather than formed with strategy as is realistic in an actual game setting) there are 2,317,817,502,000 (2.3 trillion) 9-card combinations.
- As stated above, the highest score a dealer can get with both hand and crib considered is 53.
- The only point total between 0 and 53 that is not possible is 51.
Scoring Breakdown
| Score | Number of hand-crib pairs (out of 2,317,817,502,000) | Percentage of hand-crib pairs to 6 decimal places | Percentage of hand-crib pairs at least as high |
|---|---|---|---|
| 0 | 14,485,964,652 | 0.624983 | 100 |
| 1 | 3,051,673,908 | 0.131662 | 99.375017 |
| 2 | 80,817,415,668 | 3.486789 | 99.243356 |
| 3 | 23,841,719,688 | 1.028628 | 95.756566 |
| 4 | 190,673,505,252 | 8.226424 | 94.727938 |
| 5 | 70,259,798,952 | 3.031291 | 86.501514 |
| 6 | 272,593,879,188 | 11.7608 | 83.470222 |
| 7 | 121,216,281,624 | 5.22976 | 71.709422 |
| 8 | 290,363,331,432 | 12.527446 | 66.479663 |
| 9 | 151,373,250,780 | 6.530853 | 53.952217 |
| 10 | 254,052,348,948 | 10.960843 | 47.421364 |
| 11 | 141,184,445,960 | 6.091267 | 36.460521 |
| 12 | 189,253,151,324 | 8.165145 | 30.369254 |
| 13 | 98,997,926,340 | 4.27117 | 22.204109 |
| 14 | 127,164,095,564 | 5.486372 | 17.932939 |
| 15 | 59,538,803,512 | 2.568744 | 12.446567 |
| 16 | 77,975,659,056 | 3.364185 | 9.877823 |
| 17 | 32,518,272,336 | 1.402969 | 6.513638 |
| 18 | 42,557,293,000 | 1.836093 | 5.110669 |
| 19 | 17,654,681,828 | 0.761694 | 3.274576 |
| 20 | 22,185,433,540 | 0.957169 | 2.512881 |
| 21 | 8,921,801,484 | 0.384923 | 1.555712 |
| 22 | 10,221,882,860 | 0.441013 | 1.17079 |
| 23 | 4,016,457,976 | 0.173286 | 0.729776 |
| 24 | 5,274,255,192 | 0.227553 | 0.55649 |
| 25 | 1,810,154,696 | 0.078097 | 0.328938 |
| 26 | 2,305,738,180 | 0.099479 | 0.25084 |
| 27 | 750,132,024 | 0.032364 | 0.151361 |
| 28 | 1,215,878,408 | 0.052458 | 0.118998 |
| 29 | 401,018,276 | 0.017302 | 0.06654 |
| 30 | 475,531,940 | 0.020516 | 0.049238 |
| 31 | 184,802,724 | 0.007973 | 0.028722 |
| 32 | 233,229,784 | 0.010062 | 0.020749 |
| 33 | 82,033,028 | 0.003539 | 0.010686 |
| 34 | 71,371,352 | 0.003079 | 0.007147 |
| 35 | 19,022,588 | 0.000821 | 0.004068 |
| 36 | 44,459,120 | 0.001918 | 0.003247 |
| 37 | 9,562,040 | 0.000413 | 0.001329 |
| 38 | 10,129,244 | 0.000437 | 0.000916 |
| 39 | 1,633,612 | 0.00007 | 0.000479 |
| 40 | 5,976,164 | 0.000258 | 0.000409 |
| 41 | 1,517,428 | 0.000065 | 0.000151 |
| 42 | 600,992 | 0.000026 | 0.000085 |
| 43 | 127,616 | 0.000006 | 0.00006 |
| 44 | 832,724 | 0.000036 | 0.000054 |
| 45 | 222,220 | 0.00001 | 0.000018 |
| 46 | 42,560 | 0.000002 | 0.000009 |
| 47 | 24,352 | 0.000001 | 0.000007 |
| 48 | 119,704 | 0.000005 | 0.000006 |
| 49 | 6,168 | 0 | 0 |
| 50 | 384 | 0 | 0 |
| 51 | 0 | 0 | 0 |
| 52 | 4,320 | 0 | 0 |
| 53 | 288 | 0 | 0 |
- Mean: 9.50397
- Median: 9
- Mode: 8
See also[edit]
References[edit]
- ^ abcSteven S. Lumetta (2007-05-15). 'Amusing Cribbage Facts'. Archived from the original on 2018-01-16. Retrieved 2008-03-03.
- ^Tim Wood (2008-08-05). 'All Possible Cribbage Hands'. Archived from the original on 2013-02-09. Retrieved 2008-08-05.
- ^ abWeisstein, Eric W. 'Cribbage'. MathWorld. Retrieved 2008-03-02.
All scores from 0 to 29 are possible, with the exception of 19, 25, 26, and 27. For this reason, hand scoring zero points is sometimes humorously referred to as a '19-point' hand.
- ^Cribbage Corner (2008-05-05). 'Perfect cribbage hand odds'. Retrieved 2008-05-05.